Selamat Datang

CARA MUDAH MENGINGAT NILAI PERBANDINGAN TRIGONOMETRI

SUDUT ISTIMEWA DENGAN TANGAN

 

Matematika adalah pelajaran yang sangat penting dalam kehidupan sehari-hari. Tapi pada kenyataannya banyak siswa yang tidak menyukai bahkan beranggapan bahwa matematika itu pelajaran yang menyulitkan. Hal ini bisa terjadi karena siswa kurang memahami konsep materi yang disampaikan oleh guru dan penyampaian materi juga kurang menarik perhatian siswa selama proses pembelajaran. Sehingga banyak siswa yang kurang tertarik terhadap pelajaran matematika. Pembelajaran matematika seharusnya berpusat pada siswa, bukan pada guru. Belajar matematika merupakan proses mengkonstruksi konsep-konsep dan prinsip -prinsip yang saling berkaitan satu sama lain. Memahami konsep merupakan kemampuan siswa dalam melakukan prosedur (algoritma) secara luwes, akurat, efisien dan tepat (Asep Jihad dan Abdul Haris, 2010: 149).

Begitu juga halnya dengan materi trigonometri, banyak siswa yang mengeluh ketika harus mempelajari materi trigonometri. Hal tersebut sebagian besar dikarenakan banyaknya rumus dalam

materi trigonometri dan mereka lebih menekankan pada hafalan rumus semata tanpa mengetahui konsep dasarnya. Di samping itu mungkin dalam pembelajaran guru masih menggunakan metode yang konvesional, sehingga trigonometri bagi anak tidak menarik sama sekali.

 Oleh sebab itu perlu diterapkan pembelajaran yang menarik dan menyenangkan untuk menyampaikan materi trigonometri agar siswa lebih mudah memahami dan lebih menyukai pelajaran matematika.

Sejarah  Trigonometri

Istilah “trigonometri” berasal dari kata Yunani, trigonon yang berarti segitiga dan metria yang berarti pengukuran. Sesuai namanya, trigonometri dikembangkan dari studi mengenai segitiga siku-siku dengan menerapkan hubungan antara ukuran sisi dan sudut segitiga tersebut ke studi mengenai segitiga lain yang serupa (Syahbana, 2015:2).

Awal trigonometri dapat dilacak hingga zaman Mesir Kuno dan Babilonia dan peradaban Lembah Indus, lebih dari 3000 tahun yang lalu. Matematikawan India adalah perintis penghitungan variabel aljabar yang digunakan untuk menghitung astronomi dan juga trigonometri. Lagadha adalah matematikawan yang dikenal sampai sekarang yang menggunakan geometri dan trigonometri untuk penghitungan astronomi dalam bukunya Vedanga, Jyotisha, yang sebagian besar hasil kerjanya hancur oleh penjajah India. Matematikawan Yunani Hipparchus sekitar 150 SM menyusun tabel trigonometri untuk menyelesaikan segitiga. Matematikawan Yunani lainnya, Ptolemy sekitar tahun 100 mengembangkan penghitungan trigonometri lebih lanjut. Matematikawan Silesia Bartholemaeus Pitiskus menerbitkan sebuah karya yang berpengaruh tentang trigonometri pada 1595 dan memperkenalkan kata ini ke dalam bahasa Inggris dan Perancis.

Walaupun pada mulanya trigonometri dikaji sebagai cabang astronomi tetapi akhirnya trigonometri berdiri sendiri sebagai sebuah disiplin ilmu. Perkembangan awal trigonometri disebabkan oleh keperluan penyelesaian masalah astronomi. Kemunculan trigonometri merupakan proses yang perlahan. Jika dibandingkan dengan cabang matematika lain, trigonometri berkembang disebabkan hubungan antara pendidikan matematika terapan dengan keperluan sains dalam bidang astronomi.

Belajar Trigonometri dengan Cara yang Menyenangkan dalam Matematika

Istilah pembelajaran mengacu pada dua aktivitas yaitu mengajar dan belajar. Aktivitas mengajar berkaitan dengan apa yang dilakukan oleh guru dan aktivitas belajar berkaitan dengan siswa. Menurut Mulyasa (dalam Abduh, 2014:3), pembelajaran menyenangkan (joyfull instruction) merupakan suatu proses pembelajaran yang di dalamnya terdapat suatu kohesi yang kuat antara guru dan siswa, tanpa ada perasaan terpaksa atau tertekan. Pembelajaran menyenangkan adalah adanya pola hubungan baik antara guru dengan siswa dalam proses pembelajaran. Guru memposisikan diri sebagai mitra belajar siswa, bahkan dalam hal tertentu tidak menutup kemungkinan guru belajar dari siswanya. Dalam hal ini perlu diciptakan suasana yang demokratis dan tidak ada beban, baik guru maupun siswa dalam melakukan proses pembelajaran.

Seorang guru harus bisa menciptakan suasana belajar yang rileks, bebas dari tekanan, menarik, bisa membangkitkan minat belajar, bersemangat, perasaan gembira, sehingga siswa benar-benar bisa tertarik dan menyenangkan ketika belajar matematika. Begitu halnya pada materi trigonometri, banyak siswa yang sulit memahami materi/mengingat rumus trigonometri karena banyaknya rumus dalam materi tersebut. Untuk membangkitkan kembali minat belajar siswa dalam belajar matematika terutama dalam tigonometri. Salah satunya adalah dengan menggunakan tangan. 

Cara Mengingat Nilai Perbandingan Trigonometri

Nilai perbandingan tigonometri terdiri dari 4 kuadran, yaitu:

1. Kuadran I, yaitu 0^o < a < 90^o

2. Kuadran II, yaitu  90^o < a < 180^o

3. Kuadran III, yaitu 180^o < a < 270^o

4. Kuadran IV, yaitu 270^o < a < 360^o

 Untuk menetukan tanda perbandingan trigonometri di setiap kuadran, ingat kembali perbandingan trigonometri dari segitiga siku-siku yang diketahui salah satu sudutnya dan sisi-sisnya berdasarkan koordinat kartesius.

sin a = y/r                     cos a = x/r                    tan a = y/x

Tanda x dan y didapat berdasarkan  tempat kuadran sudut tersebut berada, sedangkan tanda r selalu bernilai positif karena merupakan hepotenusa.

1. Kuadran I      (0^o < a < 90^o, x positif, y positif)

sin ∝ (positif)            cos  ∝ (positif)          tan ∝ (positif)

2. Kuadran II      ( 90^o < a < 180^o, x negatif, y positif)

sin ∝ (positif)            cos  ∝ (negatif)          tan ∝ (negatif)

3. Kuadran III     (180^o < a < 270^o, x negatif, y negatif)

sin ∝ (negatif)           cos  ∝ (negatif)          tan ∝ (positif)

4. Kuadran IV    (270^o < a < 360^o, x positif, y negatif)

sin ∝ (negatif)           cos  ∝ (positif)           tan ∝ (negatif)

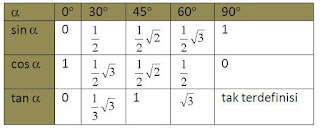
Nilai perbandingan trigonometri yang akan dibahas yaitu nilai perbandingan trigonometri untuk  sudut-sudut istimewa. Sudut-sudut istimewa itu meliputi sudut 0⁰ , 30⁰ , 45⁰ , 60⁰ , 90⁰. Agar lebih mudah mengingat nilai sin, cos, tan dari sudut-sudut istimewa, kita bisa menggunakan telapak tanga. Jadi kita tidak perlu menghafal satu-persatu nilai sin, cos, tan pada sudut-sudut. Telapak tangan yang digunakan bisa tangan kanan atau tangan kiri. Caranya sebagai berikut :

             

Pada setiap jari diumpamakan sebagai sudut-sudut istimewa yang dimulai dari ibu jari yaitu:
1. Ibu jari sebagai sudut 0⁰ ;                               4. Jari manis sebagai sudut 60⁰;
2. Jari telunjuk sebagai sudut 30⁰;                      5. Jari kelingking sebagai sudut 90⁰.
3. Jari tengah sebagai sudut 45⁰;

Pada setiap jari, terdapat sendi-sendi jari yang dalam hal ini dijadikan sebagai batas Sinus dan Cosinus. Ruas jari yang berada di tengah merupakan ruas Sinus dengan urutan nilai n sebagai berikut :

1.   Ruas ibu jari bernilai 0;                                  4. Ruas jari manis bernilai 3;

2.   Ruas telunjuk bernilai 1;                                5. Ruas kelingking bernilai 4 .

3.   Ruas jari tengah bernilai 2;

Sedangkan ruas jari terbawah sebagai ruas Cosinus dengan urutan nilai n sebagai berikut:
1. Ruas ibu jari bernilai 4;                                   4. Ruas jari manis bernilai 1;
2. Ruas telunjuk bernilai 3;                                 5. Ruas kelingking bernilai 0 .
3. Ruas jari tengah bernilai 2;
Cara Kerjanya:

a.  Sinus
Untuk mencari sinus yaitu :

Tentukan nilai n pada ruas jari. Ingat bahwa sinus berada di ruas tengah dan arahnya dimulai dari ibu jari menuju kelingking (kiri ke kanan)

Masukkan nilai n tersebut pada rumus 

Contoh :

1)  Sin 30⁰ = ..

Nilai n pada sudut 30⁰ di ruas sinus adalah 1, maka

Sin 30⁰ = ½ .  √1 = ½

2)  Sin 60⁰ = ..

Nilai n pada sudut 60⁰ di ruas sinus adalah 3, maka

Sin 60⁰ = ½ .  √3 = ½ √3

b. Cosinus

Untuk mencari nilai cosinus sama dengan sinus. Tetapi cosinus berbalik arah yaitu cosinus dari jari kelingkiling di mulai dari 0⁰.  saja arahnya berlainan. Jika sinus dari ibu jari ke kelingking, maka cosinus sebaliknya. Cara menentukannya yaitu:

Tentukan nilai n. Nilai n pada cosinus berada di bawah batas sendi.

Masukkan nilai n ke

Contoh :

1)  Cos 45⁰ = ..

Nilai n pada sudut 45⁰ di ruas cosinus adalah 2, maka
Cos 45⁰ =½ √ 2

2)  Cos 0⁰ = ..

Nilai n pada sudut 0⁰ di ruas cosinus adalah 4, maka

Cos 0⁰ =½ .  √ 4 = ½ . 2 = 1 

c.  Tangen 

Untuk menentukan nilai tangen, kita menggunakan menggunakan konsep sin dan cos.

Dengan mengunakan konsep tersebut sehingga nantinya kita bisa menyimpulkan sebagai berikut :

DAFTAR PUSTAKA

Abduh, Muhammad. 2014. Menciptakan Pembelajaran yang Menyenangkan.

https://sumsel.kemenag.go.id/files/sumsel/file/file/TULISAN/jgri1331699416.pdf diakses hari Kamis, tanggal 3 November 2016.

Jihad, Asep dan Abdul Haris. 2010. Evaluasi Pembelajaran. Yogyakarta: Multi Pressindo.

Syahbana, Ali. 2015. Trigonometri Dasar. Yogyakarta: Deepublish.